已知函数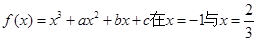 处取得极值.
处取得极值.
(1)求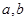 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若当 时恒有
时恒有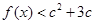 成立,求实数c的取值范围.
成立,求实数c的取值范围.
在 中,角
中,角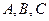 所对的边分别为
所对的边分别为 ,且
,且 .
.
(1)求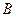 的大小;
的大小;
(2)若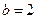 ,
, ,求
,求 的面积.
的面积.
选修4-4 :坐标系与参数方程
已知圆方程为 .
.
(1)求圆心轨迹的参数方程 ;
;
(2)点 是(1)中曲线
是(1)中曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围.
已知向量 ,动点
,动点 到定直线
到定直线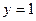 的距离等于
的距离等于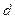 ,并且满足
,并且满足 ,其中
,其中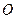 为坐标原点,
为坐标原点,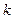 为非负实数.
为非负实数.
(1)求动点 的轨迹方程
的轨迹方程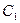 ;
;
(2)若将曲线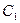 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(3)若(2)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足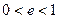 ,当
,当 是曲线
是曲线 的两个焦点时,则圆锥曲线上恒存在点
的两个焦点时,则圆锥曲线上恒存在点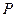 ,使得
,使得 成立,求实数
成立,求实数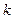 的取值范围.
的取值范围.
四棱锥 的底面为正方形,
的底面为正方形, 底面
底面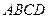 ,
,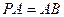 ,
, 为
为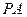 上的点.
上的点.
(1)求证:无论点 在
在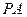 上如何移动,都有
上如何移动,都有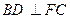 ;
;
(2)若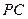 //平面
//平面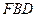 ,求二面角
,求二面角 的余弦值.
的余弦值.
已知定点A(-2,-4),过点A作倾斜角为45 的直线l,交抛物线y2=2px(p>0)于B、C两点,且|BC|=210.(Ⅰ)求抛物线的方程;(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D,使得|DB|=|DC|成立?如果存在,求出点D的坐标;如果不存在,请说明理由.