四棱锥 的底面为正方形,
的底面为正方形, 底面
底面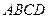 ,
,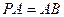 ,
, 为
为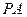 上的点.
上的点.
(1)求证:无论点 在
在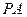 上如何移动,都有
上如何移动,都有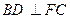 ;
;
(2)若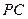 //平面
//平面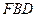 ,求二面角
,求二面角 的余弦值.
的余弦值.
设函数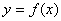 是定义在
是定义在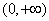 上的减函数,并且满足
上的减函数,并且满足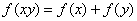 ,
,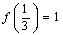
(1)求 ,
,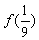 ,
,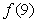 的值,(2)如果
的值,(2)如果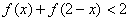 ,求x的取值范围。
,求x的取值范围。
 ,
,
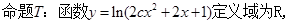
(1)若命题T为真命题,求c的取值范围。
(2)若P或Q为真命题,P且Q为假命题,求c的取值范围.
已知集合A=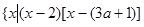
 ,集合B=
,集合B=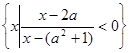 。
。
当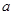 =2时,求
=2时,求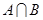 ;
;
当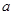
 时,若元素
时,若元素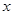
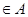 是
是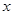
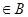 的必要条件,求实数
的必要条件,求实数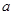 的取值范围。
的取值范围。
(本小题满分12分)四棱锥 中,底面
中,底面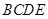 为矩形,侧面
为矩形,侧面 底面
底面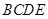 ,
,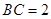 ,
,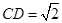 ,
,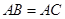 .
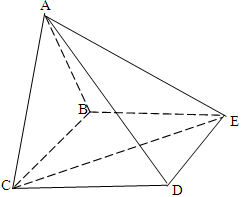
.
(Ⅰ)证明: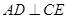 ;
;
(Ⅱ)设 与平面
与平面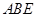 所成的角为
所成的角为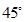 ,
,
求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且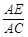 =
=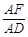 =λ (0<λ<1).
=λ (0<λ<1).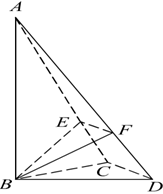
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时?平面BEF⊥平面ACD.