已知 ,(1)用列举法表示集合A;(2)写出集合A的所有子集
,(1)用列举法表示集合A;(2)写出集合A的所有子集
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
选修4-5:不等式选讲
已知函数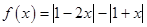
(1)解不等式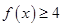 ;
;
(2)若函数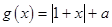 的图象恒在函数
的图象恒在函数 的图象的上方,求实数
的图象的上方,求实数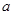 的取值范围.
的取值范围.
选修4-4:极坐标与参数方程
在极坐标系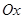 中,直线
中,直线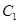 的极坐标方程为
的极坐标方程为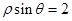 ,
,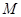 是
是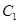 上任意一点,点
上任意一点,点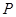 在射线
在射线 上,且满足
上,且满足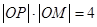 ,记点
,记点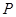 的轨迹为
的轨迹为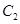 .
.
(1)求曲线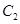 的极坐标方程;
的极坐标方程;
(2)求曲线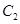 上的点到直线
上的点到直线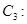
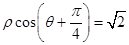 的距离的最大值.
的距离的最大值.
设函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)当 时,
时, 的最大值为
的最大值为 ,求
,求 的取值范围.
的取值范围.
已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.