如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形, AF∥DE,AF⊥FE,AF=AD=2 DE=2.
(Ⅰ) 求异面直线EF与BC所成角的大小;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为 ,求AB的长.
,求AB的长.
在△ 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
.
(Ⅰ)若 ,求角
,求角 ;
;
(Ⅱ)设 ,
, ,试求
,试求 的最大值.
的最大值.
设函数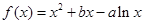
(1)若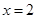 是函数
是函数 的极值点,
的极值点,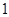 和
和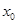 是函数
是函数 的两个不同零点,且
的两个不同零点,且 ,求
,求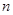 ;
;
(2)若对任意 ,都存在
,都存在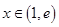 (
(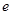 为自然对数的底数),使得
为自然对数的底数),使得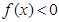 成立,求实数
成立,求实数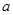 的取值范围.
的取值范围.
设等比数列 的首项为
的首项为 ,公比为
,公比为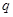 (
(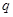 为正整数),且满足
为正整数),且满足 是
是 与
与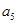 的等差中项;数列
的等差中项;数列 满足
满足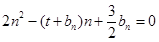 (
(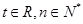 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定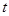 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数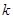 ,在
,在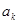 与
与 之间插入
之间插入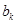 个2,得到一个新数列
个2,得到一个新数列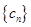 . 设
. 设 是数列
是数列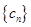 的前
的前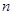 项和,试求满足
项和,试求满足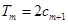 的所有正整数
的所有正整数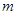 .
.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角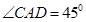 .
.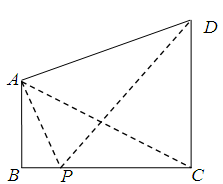
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为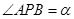 ,
,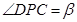 ,问点P在何处时,
,问点P在何处时, 最小?
最小?
已知数列 满足:
满足: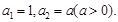 数列
数列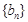 满足
满足 。
。
(1)若 是等差数列,且
是等差数列,且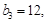 求
求 的值及
的值及 的通项公式;
的通项公式;