已知椭圆 :
:
 过点
过点 ,上、下焦点分别为
,上、下焦点分别为 、
、 ,
,
向量 .直线
.直线 与椭圆交于
与椭圆交于 两点,线段
两点,线段 中点为
中点为 .
.
(1)求椭圆 的方程;
的方程;
(2)求直线 的方程;
的方程;
(3)记椭圆在直线 下方的部分与线段
下方的部分与线段 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为 ,若曲线
,若曲线 与区域
与区域 有公共点,试求
有公共点,试求 的最小值.
的最小值.
((本小题满分12分)
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于 +1 (n∈N*), 则算过关.
+1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2)若规定n≤3, 求某人的过关数ξ的期望.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分别为AB、PC的中点。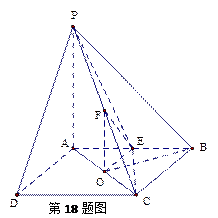
(1)求异面直线PA与BF所成角的正切值。
(2)求证:EF⊥平面PCD。
(本小题满分10分)
已知函数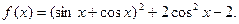
(1)求函数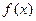 的最小正周期T;
的最小正周期T;
(2)当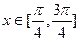 时,求函数
时,求函数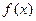 的最大值和最小值。
的最大值和最小值。
如图,直四棱柱 中,底面
中,底面 是
是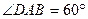
 的菱形,
的菱形,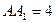 ,
,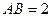 ,点
,点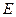 在棱
在棱 上,点
上,点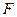 是棱
是棱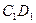 的中点.
的中点.
(1)若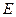 是
是 的中点,求证:
的中点,求证: ;
;
(2)求出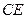 的长度,使得
的长度,使得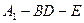 为直二面角.
为直二面角.
.若以连续掷两次骰子分别得到的点数m、 n作为点P的坐标
n作为点P的坐标 ,求:
,求: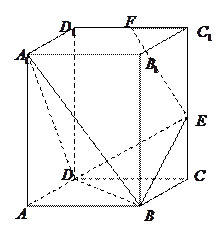
(1)点P在直线 上的概率;
上的概率;
(2)点P在圆 外的概率.
外的概率.