如图,AB是⊙O的直径,C、E为⊙O上的点,CA平分∠BAE,CF⊥AB, F是垂足,CD⊥AE,交AE延长线于D.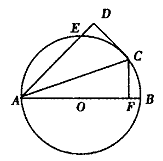
(I)求证:DC是⊙O的切线;
(Ⅱ)求证:AF.FB=DE.DA.
如图,在四棱柱ABCD-A1B1C1D1中,已 知平面AA1C1C丄平面ABCD,且AB=BC=CA= , AD =" CD" =1
, AD =" CD" =1
(I)求证:BD丄AA1;
(II)若四边形ACC1A1是菱形,且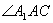 =600,求四棱柱 ABCD-A1B1C1D1的体积.
=600,求四棱柱 ABCD-A1B1C1D1的体积.
数列{an}是公比为 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( 为常数,且
为常数,且 ≠1).
≠1).
(I)求数列{an}的通项公式及 的值;
的值;
(Ⅱ)比较 +
+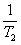 +
+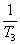 + +
+ +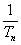 与了
与了 Sn的大小.
Sn的大小.
已知向量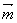 =(
=(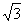 sin2x+2,cosx),
sin2x+2,cosx), =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 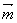 ·
· .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若A=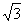 ,b=f(
,b=f( ),ΔABC的面积为
),ΔABC的面积为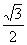 ,求a的值
,求a的值
已知函数
⑴解不等式 ;
;
⑵若不等式 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为 .
.
⑴求圆C的极坐标方程;
⑵ 是圆
是圆 上一动点,点
上一动点,点 满足
满足 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.