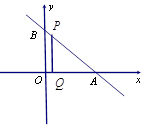
(本小题10分)如图直线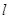 过点(3,4), 与
过点(3,4), 与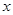 轴、
轴、 轴的正半轴分别交于A、B两点,△ABC的面积为24. 点
轴的正半轴分别交于A、B两点,△ABC的面积为24. 点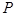 为线段
为线段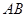 上一动点,且
上一动点,且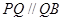 交
交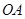 于点
于点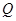 .
.
(Ⅰ)求直线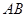 斜率的大小;
斜率的大小;
(Ⅱ)若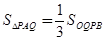 时,请你确定
时,请你确定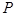 点在
点在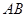 上的位置,并求出线段
上的位置,并求出线段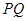 的长;
的长;
(Ⅲ)在 轴上是否存在点
轴上是否存在点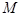 ,使△
,使△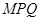 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点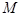 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分13分)
如图,过抛物线 (
(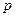 >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
(本小题满分12分)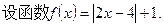


(本小题满分12分)
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求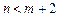 的概率.
的概率.
(本小题满分12分)已知函数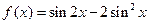
(Ⅰ)求函数 的最小正周期。
的最小正周期。
(Ⅱ)求函数 的最大值及
的最大值及 取最大值时x的集合。
取最大值时x的集合。
设函数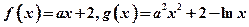 ,其中
,其中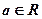 ,
,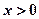 。
。
(1)若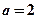 ,求曲线
,求曲线 在
在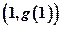 点处的切线方程;
点处的切线方程;
(2)是否存在负数 ,使
,使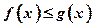 对一切正数
对一切正数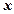 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。