(本小题满分13分)
如图,过抛物线 (
(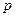 >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
已知椭圆C: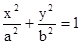 (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N.
①求椭圆C的方程.
②当⊿AMN的面积为 时,求k的值.
时,求k的值.
已知函数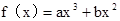 ,曲线
,曲线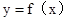 过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直。
过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直。
①求a,b的值;
②求该函数的单调区间和极值。
③若函数在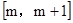 上是增函数,求m的取值范围.
上是增函数,求m的取值范围.
已知命题P: 命题Q:
命题Q: <0.若命题P是真命题,命题Q是假命题,求实数x的取值范围.
<0.若命题P是真命题,命题Q是假命题,求实数x的取值范围.
已知函数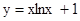
①求这个函数的导数;
②求这个函数的图象在点x=1处的切线方程.
双曲线的离心率等于 ,且与椭圆
,且与椭圆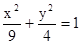 有公共焦点,
有公共焦点,
①求此双曲线的方程.
②若抛物线的焦点到准线的距离等于椭圆的焦距,求该抛物线方程.