在直角坐标系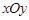
中，以原点
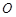为极点，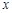
轴的正半轴为极轴建立极坐标系．已知曲线
（
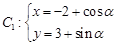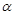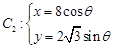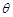为参数），
（
为参数）．
（1）将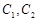
的方程化为普通方程，并说明它们分别表示什么曲线；
（2）若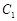
上的点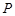
对应的参数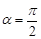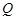为
，
为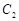
上的动点，求
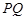中点
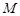到直线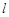
：
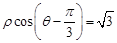的距离的最大值．
（本小题满分13分）已知M（
，0），N（2，0），曲线C上的任意一点P满足:
．
（Ⅰ）求曲线C的方程；
（Ⅱ）设曲线C与x轴的交点分别为A、B，过N的任意直线（直线与x轴不重合）与曲线C交于R、Q两点,直线AR与BQ交于点S．问：点S是否在同一直线上?若是,请求出这条直线的方程；若不是,请说明理由．
（本小题满分13分）已知数列
的首项
，其前
和为
，且满足：
（
N*）．
（Ⅰ）求数列
的通项公式；
（Ⅱ）对任意的N*，
，求实数a的取值范围．
（本小题满分12分）如图，在长方体ABCD-A1B1C1D1中，AA1=AB=2AD=2，E为AB的中点，F为D1E上的一点，D1F=2FE．
（Ⅰ）证明：平面
平面
；
（Ⅱ）求二面角
的平面角的余弦值．
（本小题满分12分）某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分，初赛采用选手从备选题中选一题答一题的方式进行；每位选手最多有5次答题机会，选手累计答对3题或答错3题即终止比赛，答对3题者直接进入复赛，答错3题者则被淘汰．已知选手甲答对每个题的概率均为
，且相互间没有影响．
（Ⅰ）求选手甲进入复赛的概率；
（Ⅱ）设选手甲在初赛中答题的个数为，试求的分布列和数学期望．
（本小题满分12分）在△ABC中，内角
，
，
的对边长分别为a，b，c，且
．
（Ⅰ）求角的大小；
（Ⅱ）若a＝3，
，求△ABC的面积．