如图,三棱柱 的所有棱长都为
的所有棱长都为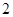 ,且
,且 平面
平面 ,
, 为
为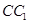 中点.
中点.
(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求二面角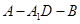 的大小的余弦值;
的大小的余弦值;
(Ⅲ)求点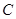 到平面
到平面 的距离.
的距离.
已知函数
在
时取得最大值4.
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
,求
.
已知a,b,c,分别是三角形的三个内叫角A,B,C所对的边,若a=1b=根号3A+C=2B,求sinC的值
若向量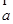 =(1,1,x),
=(1,1,x), 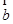 =(1,2,1),
=(1,2,1),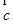 =(1,1,1),满足条件
=(1,1,1),满足条件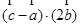 =-2,则
=-2,则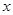 =.
=.
函数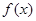 =lg(
=lg( -2)的定义域是 .
-2)的定义域是 .
(1)已知矩阵M=
,N=
,且MN=
。
(Ⅰ)求实数
的值;
(Ⅱ)求直线
在矩阵
所对应的线性变换作用下的像的方程。
(2)在直角坐标系
中,直线
的参数方程为
(
为参数),在极坐标系(与直角坐标系
取相同的长度单位,且以原点
为极点,以
轴正半轴为极轴)中,圆
的方程为
。
(Ⅰ)求圆
的直角坐标方程;
(Ⅱ)设圆
与直线
交于点
。若点
的坐标为(
),求
。
(3)已知函数
.
(Ⅰ)若不等式
的解集为
,求实数
的值;
(Ⅱ)在(Ⅰ)的条件下,若
对一切实数
恒成立,求实数
的取值范围。