已知圆心为C的圆经过点A(-1,1)和B(-2,-2),且圆心在直线L:x+y-1=0上,求圆心为C的圆的标准方程.
(本小题满分12分)
已知数列 中,
中,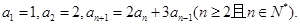
(I)证明数列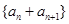 是等比数列;
是等比数列;
(II)求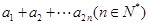
(本小题12分)
已知函数 ,
,

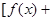

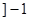 ,
, 是
是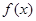 的导函数.
的导函数.
(I)若 ,求
,求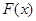 的值;(Ⅱ)求
的值;(Ⅱ)求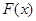 的单调减区间.
的单调减区间.
(本小题满分12分)
如图所示,正方形 与直角梯形
与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求四面体 的体积.
的体积.
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘,得分记为 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).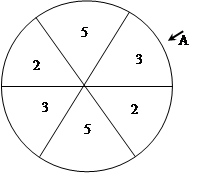
(Ⅰ)请列出一个家庭得分 的所有情况;
的所有情况;
(Ⅱ)若游戏规定:一个家庭的总得分为参与游戏的两人所得分数之和,且总得分为偶数的家庭可以获得一份奖品.请问一个家庭获奖的概率为多少?
选修4—5:不等式选讲
设函数
(1)当a=4时,求不等式 的解集
的解集
(2)若 对
对 恒成立,求a的取值范围。
恒成立,求a的取值范围。