在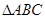 中,已知
中,已知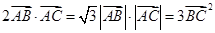 ,求角
,求角 的大小.
的大小.
已知A、B、C是三角形ABC的三内角,且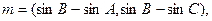
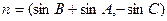 ,并且
,并且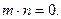
(1)求角A的大小。
(2)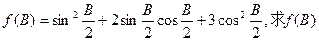 的递增区间。
的递增区间。
某工厂2010年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会:
(1)问A、B、C、D型号的产品各抽取多少件?
(2)从50件样品随机的抽取2件,求这2件产品恰好是不同型号产品的概率; (3)从A、C型号的产品中随机的抽取3件,用
(3)从A、C型号的产品中随机的抽取3件,用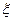 表示抽取A种型号的产品件数,求
表示抽取A种型号的产品件数,求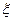 的分布列和数学期望。
的分布列和数学期望。
(22、23、24三题中任选一题作答,如果多做,则按所做的的第一题记分)
(本小题满分10分)选修4—5:不等式选讲
设函数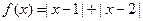
(1)求不等式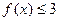 的解集;
的解集;
(2)若不等式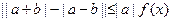 (
(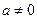 ,
,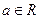 ,
,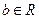 )恒成立,求实数
)恒成立,求实数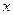 的范围.
的范围.
(22、23、24三题中任选一题作答,如果多做,则按所做的的第一题记分)
(本小题满分10分)选修4—4:坐标系与参数方程已知直线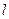 的参数方程为
的参数方程为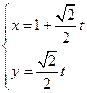 (
(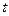 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是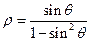 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点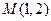 ,直线
,直线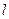 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线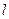 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求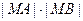 的值.
的值.
(22、23、24三题中任选一题作答,如果多做,则按所做的的第一题记分)(本小题满分10分)选修4—1:几何证明选讲
如图, 是⊙
是⊙ 的直径,弦CA、BD的延长线相交于点E,EF垂直BA的延长线于点F.
的直径,弦CA、BD的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2) .
.