一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s的速度前进(如图),现在小船在水平面P点以南的40米处,汽车在桥上Q点以西30米处(其中PQ⊥水面),求小船与汽车间的最短距离(不考虑汽车与小船本身的大小).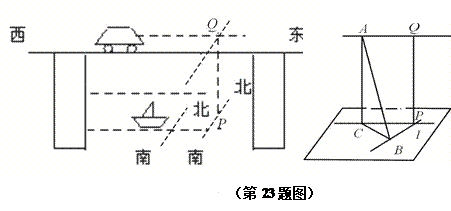
已知等差数列{ }的公差
}的公差 ,它的前n项和为
,它的前n项和为 ,若
,若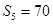 ,且
,且 成等比数列,
成等比数列,
(Ⅰ)求数列{ }的通项公式;
}的通项公式;
(Ⅱ)若数列{ }的前n项和为
}的前n项和为 ,求证:
,求证: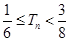 .
.
已知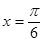 是函数
是函数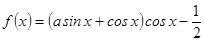 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)求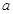 的值;
的值;
(Ⅱ)化简 的解析式,并作出函数
的解析式,并作出函数 在
在 上的图象简图(不要求写作图过程).
上的图象简图(不要求写作图过程).
已知函数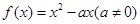 ,
,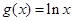 ,
,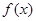 图象与
图象与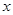 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为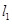 ,
,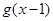 与
与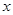 轴的交点N处的切线为
轴的交点N处的切线为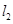 , 并且
, 并且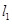 与
与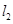 平行.
平行.
(1)已知实数t∈R,求 的取值范围及函数
的取值范围及函数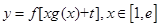 的最小值(用t表示);
的最小值(用t表示);
(2)令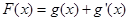 ,给定
,给定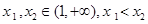 ,对于两个大于1的正数
,对于两个大于1的正数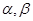 ,存在实数
,存在实数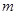 满足:
满足: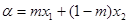 ,
,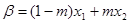 ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数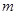 的取值范围.
的取值范围.
已知椭圆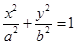 (
(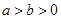 )的左、右焦点分别为
)的左、右焦点分别为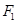 、
、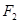 ,短轴两个端点为
,短轴两个端点为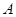 、
、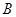 ,且四边形
,且四边形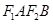 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若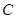 、
、 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点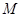 满足
满足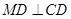 ,连结
,连结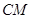 ,交椭圆于点
,交椭圆于点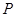 .证明:
.证明: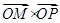 为定值;
为定值;
(3)在(2)的条件下,试问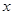 轴上是否存在异于点
轴上是否存在异于点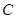 的定点Q,使得以
的定点Q,使得以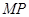 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点Q的坐标;若不存在,说明理由.
的交点,若存在,求出点Q的坐标;若不存在,说明理由.
已知等差数列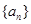 的前
的前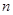 项和为
项和为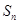 ,并且
,并且 ,
,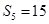 ,数列
,数列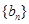 满足:
满足: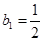 ,
,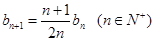 ,记数列
,记数列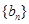 的前
的前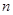 项和为
项和为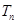 .
.
(1)求数列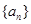 的通项公式
的通项公式 及前
及前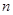 项和公式
项和公式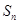 ;
;
(2)求数列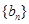 的通项公式
的通项公式 及前
及前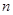 项和公式
项和公式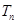 ;
;
(3)记集合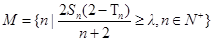 ,若
,若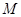 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围。
的取值范围。