(本小题满分12分)已知函数 在
在 内有极值.
内有极值.
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)若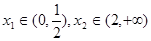 ,且
,且 时,求证:
时,求证: .
.
已知点 ,点
,点 是直线
是直线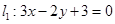 和直线
和直线 的交点.
的交点.
(1)求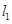 与
与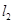 的交点
的交点 的坐标;
的坐标;
(2)求 的面积.
的面积.
若不等式 的解集为是
的解集为是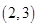 ,
,
(1)求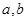 的值
的值
(2)求不等式 的解集.
的解集.
在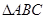 中,三内角
中,三内角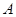 、
、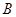 、
、 的对边分别是
的对边分别是 、
、 、
、 .
.
(1)若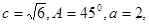 求
求 ;
;
(2)若 ,
,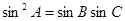 ,试判断
,试判断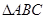 的形状.
的形状.
(本小题满分14分)设数列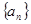 的前
的前 项和为
项和为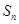 ,已知
,已知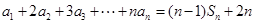
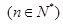 .
.
(1)求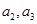 的值;
的值;
(2)求证:数列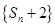 是等比数列;
是等比数列;
(3)设 ,数列
,数列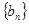 的前
的前 项和为
项和为 ,求满足
,求满足 的最小自然数
的最小自然数 的值.
的值.
(本小题满分14分)围建一个面积为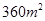 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽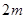 的进出口,如图2所示.已知旧墙的维修费用为
的进出口,如图2所示.已知旧墙的维修费用为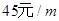 ,新墙的造价为
,新墙的造价为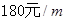 .设利用旧墙的长度为
.设利用旧墙的长度为 (单位:
(单位: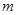 ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为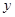 (单位:元).
(单位:元).
(1)将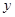 表示为
表示为 的函数,并写出此函数的定义域;
的函数,并写出此函数的定义域;
(2)若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%,试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.