如图,四棱柱 中,
中,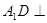 平面
平面 ,底面
,底面 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ,
,

(Ⅰ)证明: ;
;
(Ⅱ)若棱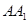 上存在一点
上存在一点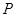 ,使得
,使得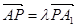 ,
,
当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
(本小题满分12分)
在
(1)求角C的大小;
(2)若AB边的长为 ,求BC边的长.
,求BC边的长.
(本小题满分12分)
已知函数
(1)确定 上的单调性;
上的单调性;
(2)设 在(0,2)上有极值,求
在(0,2)上有极值,求 的取值范围。
的取值范围。
(本小题满分12分)
已知半圆 ,动圆与此半圆相切且与
,动圆与此半圆相切且与 轴相切。
轴相切。
(1)求动圆圆心的轨迹,并画出其轨迹图形;
(2)是否存在斜率为 的直线
的直线 ,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足
,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足 。若存在,求出
。若存在,求出 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
在△ABC中, 的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)
的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)
(1)若F是AB的中点,求证:平面ACD⊥平面ADE
(2)P是AC上任意一点,求证:平面ACD⊥平面PBE
(3)P是AC上一点,且AC⊥平面PBE,求二面角P-BE-C的大小