如图,几何体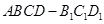 中,四边形
中,四边形 为菱形,
为菱形, ,
, ,面
,面 ∥面
∥面 ,
, 、
、 、
、 都垂直于面
都垂直于面 ,且
,且 ,
, 为
为 的中点.
的中点.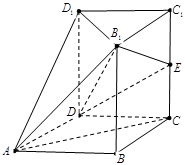
(Ⅰ)求证: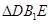 为等腰直角三角形;
为等腰直角三角形;
(Ⅱ)求证: ∥面
∥面 .
.
 和
和 的极坐标方程分别为
的极坐标方程分别为 .
.
(Ⅰ)把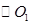 和
和 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过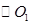 ,
, 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
把下列参数方程化为普通方程,并说明它们各表示什么曲线:
⑴ (
(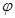 为参数);⑵
为参数);⑵ (
( 为参数)
为参数)
已知实数a满足0<a≤2,a≠1,设函数f (x)= x3-
x3- x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ)若函数g(x)=x3+bx2-(2b+4)x+ln x (b∈R)的极小值点与f (x)的极小值点相同.
求证:g(x)的极大值小于等于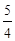 .
.
过点 作直线
作直线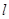 与抛物线
与抛物线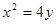 相交于两点
相交于两点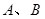 ,圆
,圆
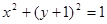
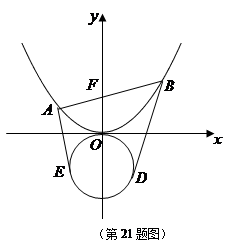
(Ⅰ)若抛物线在点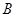 处的切线恰好与圆
处的切线恰好与圆 相切,求直线
相切,求直线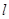 的方程;
的方程;
(Ⅱ)过点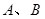 分别作圆
分别作圆 的切线
的切线 ,试求
,试求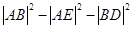 的取值范围.
的取值范围.
如图,在四棱锥P-ABCD中,PA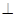 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:CD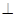 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于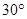 ,求k的取值范围.
,求k的取值范围.