如图，在底面是正方形的四棱锥P—ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一点．
（1）求证：BD⊥FG；
（2）确定点G在线段AC上的位置，使FG//平面PBD，并说明理由．
（3）当二面角B—PC—D的大小为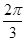
时，求PC与底面ABCD所成角的正切值．
在长方体
中，
分别是
的中点，
，过
三点的的平面截去长方体的一个角后.得到如图所示的几何体
，且这个几何体的体积为
.
（1）求证：
//平面
；
（2）求
的长；
（3）在线段
上是否存在点
，使直线
与
垂直，如果存在，求线段的长，如果不存在，请说明理由.
已知
的周长为
，且
（1）求边
的长；
（2）若的面积为
，求角
.
设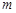
是给定的正整数，有序数组（
）中
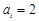或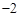
.
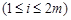（1）求满足“对任意的
，
，都有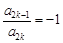
”的有序数组（）的个数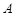
；
（2）若对任意的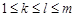
，
，
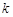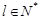，都有
成立，求满足“存在，使得
”的有序数组（）的个数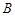
【原创】（本小题满分10分）从棱长为1的正方体的8个顶点中任取3个点，设随机变量ξ是以这三点为顶点的三角形的面积．
（1）求概率
；
（2）求ξ的分布列，并求其数学期望E（ξ ）．
（选修4—5：不等式证明选讲）已知
均为正数，证明：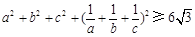
．