某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100 天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
已知曲线 的极坐标方程为
的极坐标方程为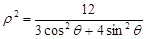 ,曲线
,曲线 经过坐标变换
经过坐标变换 得到曲线
得到曲线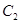 ,直线
,直线 的参数方程为
的参数方程为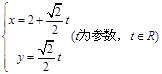
(Ⅰ)求直线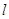 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若 为曲线
为曲线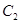 上的点,求点
上的点,求点 到直线
到直线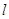 的距离的最大值。
的距离的最大值。
已知定义域为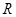 的函数
的函数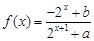 是奇函数。
是奇函数。
(Ⅰ)求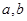 的值;
的值;
(Ⅱ)判断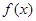 的单调性,并据此求对任意的
的单调性,并据此求对任意的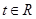 ,不等式
,不等式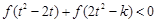 恒成立时
恒成立时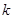 的取值范围;
的取值范围;
(本小题满分14分)设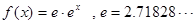 是自然对数的底.
是自然对数的底.
(1)求曲线 在点
在点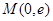 处的切线方程;
处的切线方程;
(2)设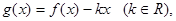 试探究函数
试探究函数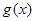 的单调性;
的单调性;
(3)若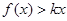 总成立,求
总成立,求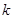 的取值范围.
的取值范围.
(本小题满分14分)已知抛物线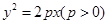 的焦 点为F,A是抛物线上横坐标为4、
的焦 点为F,A是抛物线上横坐标为4、
位于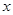 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于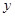 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程.
(2)以M为圆心,MB为半径作圆M,当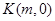 是
是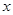 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
(本小题满分14分)已知等差数列 的各项均为正数,
的各项均为正数,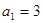 ,前n项和为Sn,数列
,前n项和为Sn,数列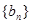 是等比数列,
是等比数列,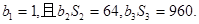
(1)求数列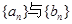 的通项公式.
的通项公式.
(2)求证: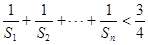 对一切
对一切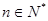 都成立.
都成立.