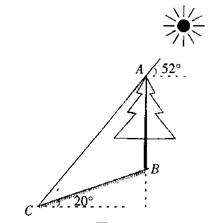
暑假期间,某学校同学积极参加社会公益活动.开学后,校团委随机抽取部分学生对每人的“累计参与时间”进行了调查,将数据整理并绘制成如图①、②所示的统计图.请根据这两幅不完整的统计图解答下列问题: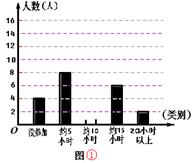
(1)这次调查共抽取了多少名学生?
(2)将图①的内容补充完整;
(3)求图②中“约15小时”对应的圆心角度数,并将图②的内容补充完整.
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
设
 ,试求k的值;
,试求k的值;如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出 的值.
的值.
已知二次函数的图象与x轴只有一个交点A(-2,0)、与y轴的交点为B(0,4),且其对称轴与y轴平行.求该二次函数的解析式,并在所给坐标系中画出它的大致图象;
在二次函数位于A、B两点之间的图象上取一点M,过点M分别作x轴、y轴的垂线,垂足分别为点C、D.求矩形MCOD的周长的最小值和此时的点M的坐标.

某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
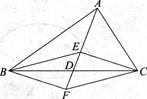
如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.求证:△BDF≌△CDE;
若AB=AC,求证:四边形BFCE是菱形.
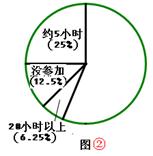
如图,在一个坡角为20º的斜坡上方有一棵树,高为AB,当太阳光线与水平线成52º角时,测得该树在斜坡上的树影BC的长为10m,求树高AB(精确到0.1m).
(已知:sin20º≈0.342,cos20º≈0.940,tan20º≈0.364,sin52º≈0.788,cos52º≈0.616,tan52º≈1.280)