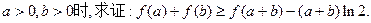“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
 10 10 |
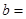 |
|
| 不反感 |
 |
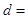 8 8 |
|
| 合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是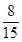 .
.
(Ⅰ)请将上面的2×2列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
参考数据和公式:
2×2列联表 公式:
公式: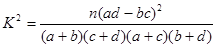 ,
, 的临界值表:
的临界值表:
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分14分)
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O: 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
.(本小题满分14分)
如图7,在直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, 是
是 的中点.
的中点.
(1)求证: ;(2)求三棱锥
;(2)求三棱锥 的体积;(3)求二面角
的体积;(3)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 个数据按照区间
个数据按照区间 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图
(1)若已知 位居民中月均用水量小于1吨的人数是12,求
位居民中月均用水量小于1吨的人数是12,求 位居民中月均用水量分别在区间
位居民中月均用水量分别在区间 和
和 内的人数;
内的人数;
(2)在该市居民中随意抽取10位,求至少有2位居民月均用水量在区间 或
或 内的概率.(精确到0.01.参考数据:
内的概率.(精确到0.01.参考数据: )
)
在锐角三角形 中,BC=1,
中,BC=1, ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
(本小题满分14分)已知函数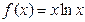
(I)求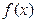 的最小值;
的最小值;
(II)讨论关于x的方程 的解的个数;
的解的个数;
(III)当