某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 |
1至4件 |
5至8件 |
9至12件 |
13至16件 |
17件及以上 |
| 顾客数(人) |
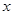 |
30 |
25 |
 |
10 |
| 结算时间(分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)
已知椭圆 :
: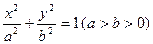 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 相交于
相交于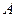 、
、 ,
, .
.
⑴求 、
、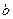 的值;
的值;
⑵若动圆 与椭圆
与椭圆 和直线
和直线 都没有公共点,试求
都没有公共点,试求 的取值范围.
的取值范围.
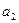 ,
, 是方程
是方程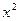
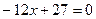 的两根, 数列
的两根, 数列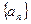 是公差为正的等差数列,数列
是公差为正的等差数列,数列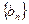 的前
的前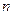 项和为
项和为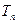 ,且
,且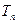
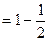
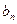
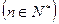 .
.
(1)求数列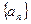 ,
,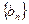 的通项公式;
的通项公式;
(2)记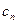 =
=
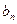 ,求数列
,求数列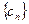 的前
的前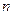 项和
项和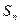 .
.
如图,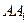 、
、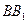 为圆柱
为圆柱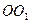 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,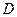 、
、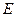 分别是
分别是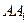 、
、 的中点,
的中点,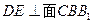 .
.
(1)证明: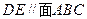 ;
;
(2)求四棱锥 与圆柱
与圆柱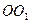 的体积比;
的体积比;
(3)若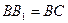 ,求
,求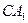 与面
与面 所成角的正弦值.
所成角的正弦值.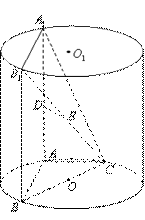
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,
他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知函数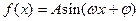
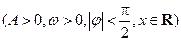 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数 的解析式;
的解析式;
(2)当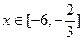 时,求函数
时,求函数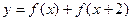 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.