“肇实,正名芡实,因肇庆所产之芡实颗粒大、药力强,故名。”某科研所为进一步改良肇实,为此对肇实的两个品种(分别称为品种A和品种B)进行试验.选取两大片水塘,每大片水塘分成n小片水塘,在总共2n小片水塘中,随机选n小片水塘种植品种A,另外n小片水塘种植B.
(1)假设n=4,在第一大片水塘中,种植品种A的小片水塘的数目记为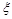 ,求
,求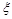 的分布列和数学期望;
的分布列和数学期望;
(2)试验时每大片水塘分成8小片,即n=8,试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位:kg/亩)如下表:
| 号码 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 品种A |
101 |
97 |
92 |
103 |
91 |
100 |
110 |
106 |
| 品种B |
115 |
107 |
112 |
108 |
111 |
120 |
110 |
113 |
分别求品种A和品种B的每亩产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
(本小题满分10分)
已知在直角坐标系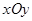 中,圆锥曲线
中,圆锥曲线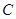 的参数方程为
的参数方程为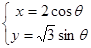 (
( 为参数),定点
为参数),定点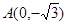 ,
,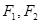 是圆锥曲线
是圆锥曲线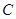 的左,右焦点.
的左,右焦点.
(Ⅰ)以原点为极点、 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线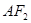 的直线
的直线 的极坐标方程;
的极坐标方程;
(Ⅱ)在(I)的条件下,设直线 与圆锥曲线
与圆锥曲线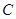 交于
交于 两点,求弦
两点,求弦 的长.
的长.
(本小题满分10分)
如图,AD是⊙O的直径,AB是⊙O的切线,M, N是圆上两点,直线MN交AD的延长线于点C,交⊙O的切线于B,BM=MN=NC=1,求AB的长和⊙O的半径.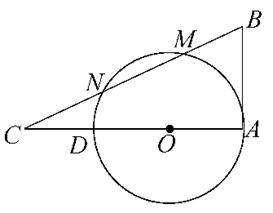
(本小题满分12分)
A﹑B﹑C是直线 上的三点,向量
上的三点,向量 ﹑
﹑ ﹑
﹑ 满足:
满足: -[y+2
-[y+2 ]·
]· +ln(x+1)·
+ln(x+1)· =
= ;
;
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0, 证明f(x)>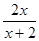 ;
;
(Ⅲ)当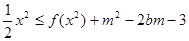 时,x
时,x
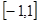 及b
及b
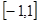 都恒成立,求实数m的取值范围。
都恒成立,求实数m的取值范围。
(本小题满分12分)
已知抛物线C1:y2=4x的焦点与椭圆C2: 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;
(Ⅰ)在 ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求 ABC重心G的轨迹方程;
ABC重心G的轨迹方程;
(Ⅱ)若P是抛物线C1与椭圆C2的一个公共点,且∠PF1F2=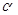 ,∠PF2F1=
,∠PF2F1=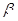 ,求cos
,求cos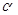
 的值及
的值及 PF1F2的面积。
PF1F2的面积。
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施.若实施方案一,预计第一年可以使出口额恢复到危机前的1.0倍、0.9倍、0.8倍的概率分别为0.3、0.3、0.4;第二年可以使出口额为第一年的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使出口额恢复到危机前的1.2倍、l.0倍、0.8倍的概率分别为0.2、0.3、0.5;第二年可以使出口额为第一年的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立.令ζ (
( =1,2)表示方案
=1,2)表示方案 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(Ⅰ)写出 、
、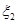 的分布列;
的分布列;
(Ⅱ)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(Ⅲ)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为10万元、15万元、20万元,问实施哪种方案的平均利润更大。