7名身高互不相等的学生，分别按下列要求排列，各有多少种不同的排法？
（1）7人站成一排，要求最高的站在中间，并向左、右两边看，身高逐个递减；
（2）任取6名学生，排成二排三列，使每一列的前排学生比后排学生矮．
已知{an}是各项均为正数的等比数列,且a1+a2=2(
+
),a3+a4+a5=64(
+
+
),
(1)求{an}的通项公式.
(2)设bn=(an+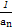
)2,求数列{bn}的前n项和Tn.
已知数列{an}中,a1=1,前n项和为Sn且Sn+1=
Sn+1,n∈N*.
(1)求数列{an}的通项公式.
(2)求数列{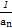
}的前n项和Tn.
已知等差数列{an}中,a2+a4=10,a5=9,数列{bn}中,b1=a1,bn+1=bn+an.
(1)求数列{an}的通项公式,写出它的前n项和Sn.
(2)求数列{bn}的通项公式.
(3)若cn=
,求数列{cn}的前n项和Tn.
数列{an}满足a1=1,an+1=(n2+n-λ)an(n=1,2,…),λ是常数.
(1)当a2=-1时,求λ及a3的值.
(2)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
等差数列{an}的各项均为正数,其前n项和为Sn,满足2S2=a2(a2+1),且a1=1.
(1)求数列{an}的通项公式.
(2)设bn=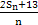
,求数列{bn}的最小值项.