国家射击队的某队员射击一次,命中7~10环的概率如下表所示:
| 命中环数 |
10环 |
9环 |
8环 |
7环 |
| 概率 |
0.32 |
0.28 |
0.18 |
0.12 |
求该射击队员射击一次
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
某射击运动员在同一条件下进行练习,结果如下表所示:
| 射击次数n |
10 |
20 |
50 |
100 |
200 |
500 |
| 击中10环次数m |
8 |
19 |
44 |
93 |
178 |
453 |
击中10环频率 |
(1)计算表中击中10环的各个频率;
(2)这位射击运动员射击一次,击中10环的概率为多少?
盒中仅有4只白球5只黑球,从中任意取出一只球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21、0.23、0.25、0.28,计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)不够7环的概率.
如图所示,矩形 和梯形 所在平面互相垂直, .
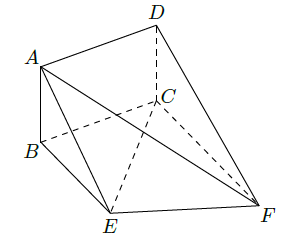
(1)求证:
平面
;
(2)当
的长为何值时,二面角
的大小为
?