已知 .
.
(1)若a=0时,求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)若函数 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(3)令 是否存在实数a,当
是否存在实数a,当 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由.
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| 围棋社 |
舞蹈社 |
拳击社 |
|
| 男生 |
5 |
10 |
28 |
| 女生 |
15 |
30 |
m |
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望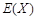 .
.
已知函数 ,记函数
,记函数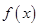 的最小正周期为
的最小正周期为 ,向量
,向量 ,
,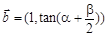 (
(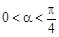 ),且
),且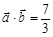 .
.
(Ⅰ)求 在区间
在区间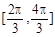 上的最值;
上的最值;
(Ⅱ)求 的值.
的值.
已知数列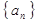 ,满足
,满足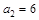 ,
,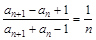
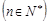 ,
,
(1)求 的值;
的值;
(2)猜想数列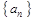 的通项公式
的通项公式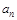 ,并用数学归纳法证明;
,并用数学归纳法证明;
(3)己知 ,设
,设 ,记
,记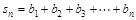 ,求
,求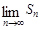 .
.
已知函数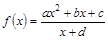 (其中
(其中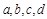 是实数常数,
是实数常数, )
)
(1)若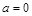 ,函数
,函数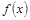 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求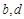 的值;
的值;
(2)若函数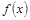 满足条件(1),且对任意
满足条件(1),且对任意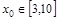 ,总有
,总有 ,求
,求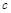 的取值范围;
的取值范围;
(3)若b=0,函数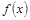 是奇函数,
是奇函数,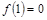 ,
,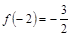 ,且对任意
,且对任意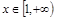 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数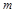 的取值范围.
的取值范围.
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数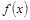 与第x天近似地满足
与第x天近似地满足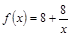 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费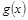 近似地满足
近似地满足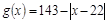 (元).
(元).
(1)求该村的第x天的旅游收入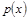 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,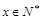 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?