某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| |
围棋社 |
舞蹈社 |
拳击社 |
| 男生 |
5 |
10 |
28 |
| 女生 |
15 |
30 |
m |
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望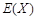 .
.
已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.(Ⅰ)求实数a,b间满足的等量关系;(Ⅱ)求线段PQ长的最小值;(Ⅲ)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.
在直角坐标系xOy中,以O为圆心的圆与直线x-3y=4相切.(1)求圆O的方程;(2)圆O与x轴相交于A,B两点,圆内的动点P使|PA|,|PO|,|PB|成等比数列,求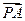 ·
· 的取值范围.
的取值范围.
某次有奖竞猜活动中,主持人准备了A`、B两个相互独立问题,并且宣布:观众答对问题A可获奖金a元,答对问题B可获奖金2a元,先答哪个问题由观众选择,只有第一个问题答对才能再答第2个问题,否则终止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为,.问你觉得应先回答哪个问题才能使你获得奖金的期望最大?说明理由。
已知数列{an}中a1=2,an+1=(-1)( an+2),n=1,2,3,….(Ⅰ)求{an}的通项公式;(Ⅱ)若数列{an}中b1=2,bn+1=,n=1,2,3,….证明:<bn≤a4n-3,n=1,2,3,…
已知{an}是正数组成的数列,a1=1,且点(,an+1)(n∈N*)在函数y=x2+1的图象上.(Ⅰ)求数列{an}的通项公式;(Ⅱ)若列数{bn}满足b1=1,bn+1=bn+2an,求证:bn ·bn+2<b2n+1.