从集合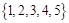
中任取三个元素构成三元有序数组
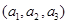，规定
.
（1）从所有的三元有序数组中任选一个，求它的所有元素之和等于10的概率
（2）定义三元有序数组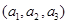的“项标距离”为
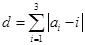（其中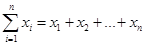
），从所有的三元有序数组中任选一个，求它的“项标距离”d为偶数的概率.
（本小题满分10分）如图，在棱长为ɑ的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．
（1）求证：平面A B1D1∥平面EFG；
（2）求证：平面AA1C⊥面EFG ．
（本小题满分10分）已知函数
(I)求
；
(Ⅱ)求函数f（x）图象的对称轴方程．
已知函数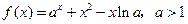
．
（I）求证：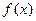
在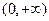
上单调递增；
（Ⅱ）函数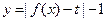
有三个零点，求
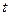值；
（Ⅲ）对
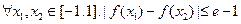恒成立，求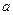
的取值范围.
（本小题满分15分）
设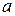
为实数，函数
.
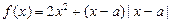(1)若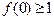
，求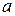的取值范围； (2)求
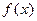的最小值．
（本小题满分14分）
已知定义域为R的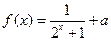函数
为奇函数。
（1）求a的值.
（2）证明函数f(x)在R上是减函数.
（3)若不等式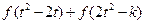
<0对任意的实数t 恒成立，求k的取值范围.