2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 |
PM2.5浓度 (微克/立方米) |
频数(天) |
频率 |
| 第一组 |
(0,25] |
5 |
0.25 |
| 第二组 |
(25,50] |
10 |
0.5 |
| 第三组 |
(50,75] |
3 |
0.15 |
| 第四组 |
(75,100) |
2 |
0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2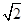 ,∠ACB=900,M是AA1的中点,N是BC1的中点.
,∠ACB=900,M是AA1的中点,N是BC1的中点.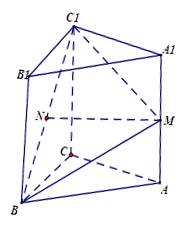
(1)求证:MN//平面A1B1C1;
(2)求二面角B-C1M-C的平面角余弦值的大小.
已知函数f(x)=Asin(ωx+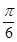 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为M(
,且图象上一个最低点为M(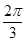 ,-2).
,-2).
(1)求f(x)的解析式;
(2)若x∈[0,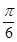 ]求函数f(x)的值域;
]求函数f(x)的值域;
(3)求函数y=f(x)的图象左移 个单位后得到的函数解析式.
个单位后得到的函数解析式.
如图2.3.1-3,MN是异面直线a、b的公垂线,平面α平行于a和b,求证:MN⊥平面α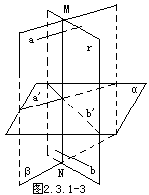
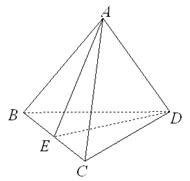
如图,设三角形ABC的三个顶点在平面 的同侧,A
的同侧,A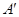 ⊥
⊥ 于
于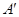 ,B
,B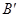 ⊥
⊥ 于
于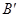 ,C
,C ⊥
⊥ 于
于 ,G、
,G、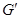 分别是△ABC和△
分别是△ABC和△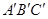 的重心,求证:G
的重心,求证:G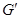 ⊥
⊥
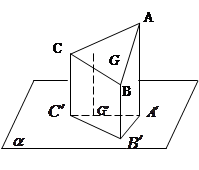
已知:空间四边形 ,
, ,
,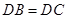 ,求证:
,求证: