如图2.3.1-3,MN是异面直线a、b的公垂线,平面α平行于a和b,求证:MN⊥平面α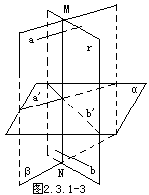
已知椭圆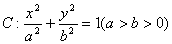 的左顶点
的左顶点 ,过右焦点
,过右焦点 且垂直于长轴的弦长为
且垂直于长轴的弦长为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点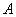 的直线
的直线 与椭圆交于点
与椭圆交于点 ,与
,与 轴交于点
轴交于点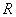 ,过原点与
,过原点与 平行的直线与椭圆交于点
平行的直线与椭圆交于点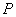 ,求证:
,求证: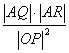 为定值.
为定值.
如图,已知 为平行四边形,
为平行四边形, ,
, ,
,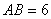 ,点
,点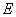 在
在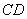 上,
上,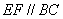 ,
, ,
, 与
与 相交于
相交于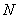 .现将四边形
.现将四边形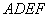 沿
沿 折起,使点
折起,使点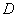 在平面
在平面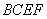 上的射影恰在直线
上的射影恰在直线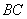 上.
上.
(Ⅰ) 求证: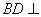 平面
平面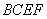 ;
;
(Ⅱ) 求折后直线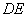 与平面
与平面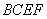 所成角的余弦值.
所成角的余弦值.
袋中有大小相同的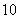 个编号为
个编号为 、
、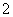 、
、 的球,
的球, 号球有
号球有 个,
个,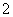 号球有
号球有 个,
个, 号球有
号球有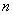 个.从袋中依次摸出
个.从袋中依次摸出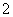 个球,已知在第一次摸出
个球,已知在第一次摸出 号球的前提下,再摸出一个
号球的前提下,再摸出一个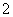 号球的概率是
号球的概率是 .
.
(Ⅰ)求 、
、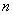 的值;
的值;
(Ⅱ)从袋中任意摸出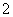 个球,记得到小球的编号数之和为
个球,记得到小球的编号数之和为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
已知函数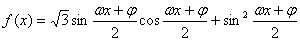
 ,
,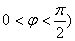 .其图象的最高点与相邻对称中心的距离为
.其图象的最高点与相邻对称中心的距离为 ,且过点
,且过点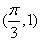 .
.
(Ⅰ)求函数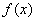 的达式;
的达式;
(Ⅱ)在△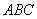 中.
中.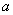 、
、 、
、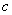 分别是角
分别是角 、
、 、
、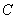 的对边,
的对边,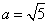 ,
,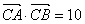 ,角C为锐角。且满足
,角C为锐角。且满足 ,求
,求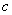 的值.
的值.
已知函数 .
.
(Ⅰ)解不等式:  ;
;
(Ⅱ)若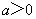 ,求证:
,求证: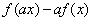 ≤
≤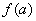 .
.