对于同一物理问题，常常可以从宏观与微观两个不同角度进行研究，-优题课

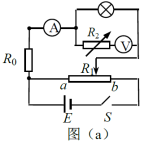
某同学用图（a）所示电路探究小灯泡的伏安特性。所用器材有:小灯泡（额定电压2.5 V，额定电流0.3 A）、电压表（量程300 mV，内阻300 Ω）、电流表（量程300 mA，内阻0.27 Ω）定值电阻 R ₀、滑动变阻器 R ₁（阻值0~20 Ω）、电阻箱 R ₂（最大阻值9 999.9 Ω）、电源 E（电动势6V，内阻不计）、开关S、导线若干。完成下列填空:

（1）有3个阻值分别为10 Ω、20 Ω、30 Ω的定值电阻可供选择，为了描绘小灯泡电流在0~300 mA的 U- I曲线， R ₀应选取阻值为______Ω的定值电阻；

（2）闭合开关前，滑动变阻器的滑片应置于变阻器的________（填" a"或" b"）端；

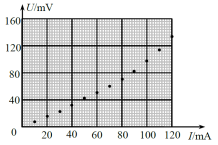
图（b）

（3）在流过电流表的电流较小时，将电阻箱 R ₂的阻值置零，改变滑动变阻器滑片的位置，读取电压表和电流表的示数 U、 I，结果如图（b）所示。当流过电流表的电流为10 mA时，小灯泡的电阻为__________Ω（保留1位有效数字）；

（4）为使得电压表满量程时对应于小灯泡两端的电压为3 V，该同学经计算知，应将 R ₂的阻值调整为_________Ω。然后调节滑动变阻器 R ₁，测得数据如下表所示：

U/mV	24.0	46.0	76.0	110.0	128.0	152.0	184.0	216.0	250.0
I/mA	140.0	160.0	180.0	200.0	220.0	240.0	260.0	280.0	300.0

（5）由图（b）和上表可知，随流过小灯泡电流的增加，其灯丝的电阻____（填"增大""减小"或"不变"）；

（6）该同学观测到小灯泡刚开始发光时流过电流表的电流为160 mA，可得此时小灯泡电功率 P ₁＝________W（保留2位有效数字）；当流过电流表的电流为300 mA时，小灯泡的电功率为 P ₂，则 $\frac{P_{2}}{P_{1}}$ =____________（保留至整数）。

单板滑雪 $U$ 型池比赛是冬奥会比赛项目，其场地可以简化为如图甲所示的模型： $U$ 形滑道由两个半径相同的四分之一圆柱面轨道和一个中央的平面直轨道连接而成，轨道倾角为 $17.2 °$ 。某次练习过程中，运动员以 $v_{M} = 10 m / s$ 的速度从轨道边缘上的 $M$ 点沿轨道的竖直切面 $ABCD$ 滑出轨道，速度方向与轨道边缘线 $AD$ 的夹角 $α = 72.8 °$ ，腾空后沿轨道边缘的 $N$ 点进入轨道。图乙为腾空过程左视图。该运动员可视为质点，不计空气阻力，取重力加速度的大小 $g = 10 m / s^{2}$ ， $\sin 72.8 ° = 0.96$ ， $\cos 72.8 ° = 0.30$ 。求：

（1）运动员腾空过程中离开 $AD$ 的距离的最大值 $d$ ；

（2） $M$ 、 $N$ 之间的距离 $L$ 。

中医拔罐的物理原理是利用玻璃罐内外的气压差使罐吸附在人体穴位上，进而治疗某些疾病。常见拔罐有两种，如图所示，左侧为火罐，下端开口；右侧为抽气拔罐，下端开口，上端留有抽气阀门。使用火罐时，先加热罐中气体，然后迅速按到皮肤上，自然降温后火罐内部气压低于外部大气压，使火罐紧紧吸附在皮肤上。抽气拔罐是先把罐体按在皮肤上，再通过抽气降低罐内气体压强。某次使用火罐时，罐内气体初始压强与外部大气压相同，温度为 $450 K$ ，最终降到 $300 K$ ，因皮肤凸起，内部气体体积变为罐容积的 $\frac{20}{21}$ 。若换用抽气拔罐，抽气后罐内剩余气体体积变为抽气拔罐容积的 $\frac{20}{21}$ ，罐内气压与火罐降温后的内部气压相同。罐内气体均可视为理想气体，忽略抽气过程中气体温度的变化。求应抽出气体的质量与抽气前罐内气体质量的比值。

如图，两侧粗细均匀、横截面积相等、高度均为 $H = 18 cm$ 的 $U$ 形管，左管上端封闭，右管上端开口。右管中有高 $h_{0} = 4 cm$ 的水银柱，水银柱上表面离管口的距离 $l = 12 cm$ 。管底水平段的体积可忽略。环境温度为 $T_{1} = 283 K$ ，大气压强 $p_{0} = 76 cmHg$ 。

$(i)$ 现从右侧端口缓慢注入水银（与原水银柱之间无气隙），恰好使水银柱下端到达右管底部。此时水银柱的高度为多少？

$(ii)$ 再将左管中密封气体缓慢加热，使水银柱上表面恰与右管口平齐，此时密封气体的温度为多少？

如图，相距 $L = 11.5 m$ 的两平台位于同一水平面内，二者之间用传送带相接。传送带向右匀速运动，其速度的大小 $v$ 可以由驱动系统根据需要设定。质量 $m = 10 kg$ 的载物箱（可视为质点），以初速度 $v_{0} = 5.0 m / s$ 自左侧平台滑上传送带。载物箱与传送带间的动摩擦因数 $μ = 0.10$ ，重力加速度取 $g = 10 m / s^{2}$ 。

（1）若 $v = 4.0 m / s$ ，求载物箱通过传送带所需的时间；

（2）求载物箱到达右侧平台时所能达到的最大速度和最小速度；

（3）若 $v = 6.0 m / s$ ，载物箱滑上传送带△ $t = \frac{13}{12} s$ 后，传送带速度突然变为零。求载物箱从左侧平台向右侧平台运动的过程中，传送带对它的冲量。