某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在"25周岁以上(含25周岁)"和"25周岁以下"分为两组,再将两组工人的日平均生产件数分为5组: , , , , ,分别加以统计,得到如图所示的频率分布直方图.
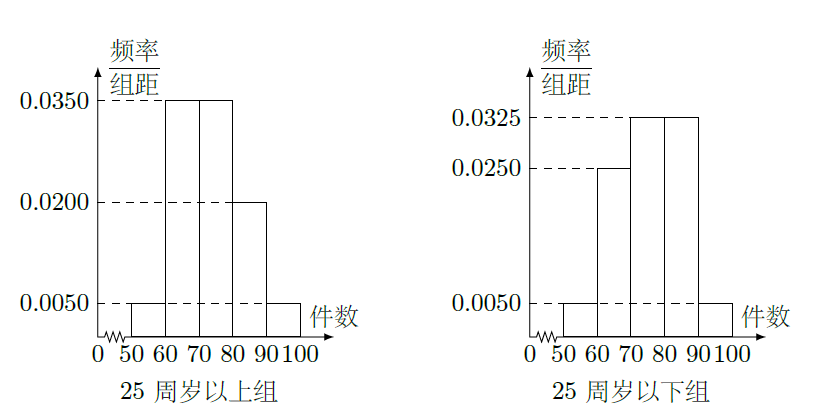
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名"25周岁以下组"工人的概率;
(II)规定日平均生产件数不少于80件者为"生产能手",请你根据已知条件完成列联表,并判断是否有90%的把握认为"生产能手与工人所在的年龄组有关"?
附: (注:此公式也可以写成 )
| 0.100 |
0.050 |
0.010 |
0.001 |
|
| 2.706 |
3.841 |
6.635 |
10.828 |
(本小题满分14分)已知函数 的导函数是
的导函数是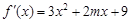 ,
, 在
在 处取得极值,且
处取得极值,且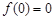 ,
,
(1)求 的极大值和极小值;
的极大值和极小值;
(2)记 在闭区间
在闭区间 上的最大值为
上的最大值为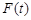 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设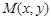 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(本小题满分13分)某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形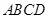 是原棚户建筑用地,测量可知边界
是原棚户建筑用地,测量可知边界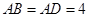 万米,
万米,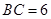 万米,
万米, 万米.
万米.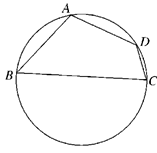
(1)请计算原棚户区建筑用地 的面积及圆面的半径
的面积及圆面的半径 的值;
的值;
(2)因地理条件的限制,边界 、
、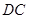 不能变更,而边界
不能变更,而边界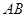 、
、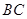 可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧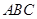 上设计一点
上设计一点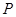 ;使得棚户区改造的新建筑用地
;使得棚户区改造的新建筑用地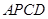 的面积最大,并求最大值.
的面积最大,并求最大值.
(本小题满分13分)若向量 其中
其中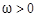 ,记函数
,记函数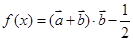 ,若函数
,若函数 的图像与直线
的图像与直线 (
( 为常数)相切,并且切点的横坐标依次成公差为
为常数)相切,并且切点的横坐标依次成公差为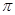 的等差数列.
的等差数列.
(1)求 的表达式及
的表达式及 的值;
的值;
(2)将函数 的图像向左平移
的图像向左平移 ,得到
,得到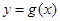 的图像,当
的图像,当 时,
时,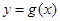 与
与 图象的交点横坐标成等比数列,求钝角
图象的交点横坐标成等比数列,求钝角 的值.
的值.
(本小题满分13分)在平面直角坐标系中,角 ,
, 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点 在角
在角 的终边上,点
的终边上,点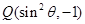 在角
在角 的终边上,且
的终边上,且 .
.
(1)求 ;
;
(2)求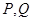 的坐标并求
的坐标并求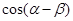 的值.
的值.
(本小题满分13分)等差数列 满足
满足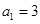 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且
,且 ,求数列
,求数列 和
和 的通项公式.
的通项公式.