如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=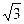
(1)求证:BC⊥SC; (2)设棱SA的中点为M,求证:DM⊥SB.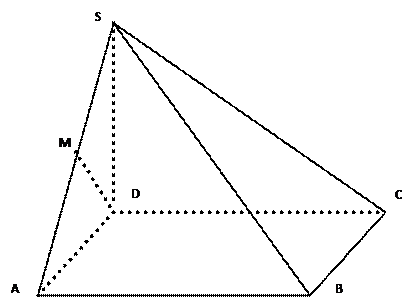
设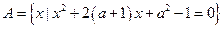 ,
,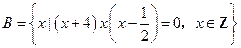 .若
.若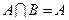 ,求
,求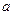 的取值范围.
的取值范围.
某校先后举行数理化三科竞赛,学生中至少参加一科的有:数学800人,物理700人,化学400人;至少参加两科的有:数学、物理500人,数学、化学300人,物理、化学200人;三种都参加的有150人,则参加竞赛的学生总人数是多少?
已知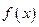 是定义在
是定义在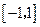 上的奇函数,且
上的奇函数,且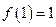 ,若
,若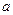 ,
, ,
,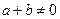 ,有
,有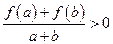 ,判断函数
,判断函数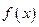 在
在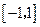 上是增函数还是减函数,并证明你的结论.
上是增函数还是减函数,并证明你的结论.
设集合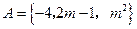 ,
,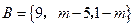 ,又
,又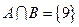 ,求实数
,求实数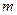 .
.
《中华人民共和国个人所得税》第十四条中有下表: 个人所得税税率表 (工资、薪金所得适用)
个人所得税税率表 (工资、薪金所得适用)
| 级数 |
全月应纳税所得额 |
税率( ) ) |
| 1 |
不超过500元 |
5 |
| 2 |
超过500元至2000元的 |
10 |
| 3 |
超过2000元至5000元的 |
15 |
| 4 |
超过5000元至20000元的 |
20 |
| 5 |
超过20000元至40000元的 |
25 |
| 6 |
超过40000元至60000元的 |
30 |
| 7 |
超过60000元至80000元的 |
35 |
| 8 |
超过80000元至100000元的 |
40 |
| 9 |
超过100000元的 |
45 |
目前,上表中“全月应纳税所得额”是从月工次、薪金收入中减去800元后的余额.
(1)请写出月工资、薪金的个人所得税 关于工资、薪金收
关于工资、薪金收
的函数解析式,并画出函数图象.
(2)某人在某月缴纳个人所得税是120元,他那个月的工资、薪金收入是多少?