在直角坐标系中，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系.已知点
的极坐标为
，直线
的极坐标方程为
，且点
在直线
上。
（Ⅰ）求
的值及直线
的直角坐标方程；
（Ⅱ）圆
的参数方程为
，试判断直线
与圆
的位置关系.
已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.
(1)当a＝－2时，求不等式f(x)<g(x)的解集；
(2)设a>－1时，且当x∈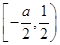
时，f(x)≤g(x)，求a的取值范围．
已知函数f(x)＝2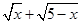
.
(1)求证：f(x)≤5，并说明等号成立的条件；
(2)若关于x的不等式f(x)≤|m－2|恒成立，求实数m的取值范围．
已知a，b为正实数．
(1)求证：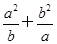
≥a＋b；
(2)利用(1)的结论求函数y＝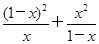
(0<x<1)的最小值．
已知函数f(x)＝|x＋3|＋|x－a|(a>0)．
(1)当a＝4时，已知f(x)＝7，求x的取值范围；
(2)若f(x)≥6的解集为{x|x≤－4或x≥2}，求a的值．
设函数f(x)＝|x－1|＋|x－2|.
(1)画出函数y＝f(x)的图象；
(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．