过抛物线
的焦点
作斜率分别为
的两条不同的直线
,且
,
与
相交于点
,
与
相交于点
.以
为直径的圆
,圆
(
为圆心)的公共弦所在的直线记为
.
(I)若
,证明;
;
(II)若点
到直线
的距离的最小值为
,求抛物线
的方程.
(本小题满分12分)如图, 在直角梯形 中,
中,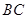 ∥
∥
点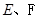 分别是
分别是 的中点,现将
的中点,现将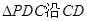 折起,使
折起,使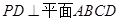 ,
,
(1)求证: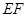 ∥平面
∥平面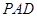 ;
;
(2)求点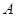 到平面
到平面 的距离.
的距离.
(本小题满分10分)已知:四边形ABCD是空间四边形,E, H分别是边AB,AD的中点,F, G分别是边CB,CD上的点,且 .
.
求证:(1)四边形EFGH是梯形;
(2)FE和GH的交点在直线AC上 .
(本小题满分8分)已知直线l垂直于直线3x-4y-7=0,直线l与两坐标轴围成的三角形的周长为10,求直线l的方程
已知数列 满足
满足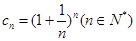 ,试证明:
,试证明:
(1)当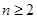 时,有
时,有 ;
;
(2) .
.
如图,在四棱锥 中,
中,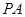 ⊥底面
⊥底面 ,底面
,底面 为梯形,
为梯形, ,
,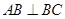 ,
,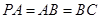 ,点
,点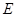 在棱
在棱 上,且
上,且 .
.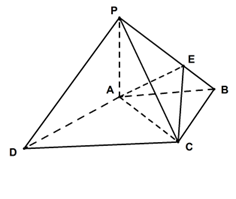
(1)求证:平面 ⊥平面
⊥平面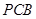 ;
;
(2)求平面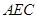 和平面
和平面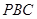 所成锐二面角的余弦值.
所成锐二面角的余弦值.