如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(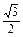 ,
, ,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
(1)求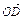 的坐标;
的坐标;
(2)设 和
和 的夹角为
的夹角为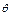 ,求cos
,求cos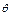 的值.
的值.
设 的导函数为
的导函数为 ,若函数
,若函数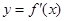 的图象关于直线
的图象关于直线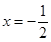 对称,且
对称,且 .
.
(Ⅰ)求实数 ,
,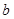 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数 的极值。
的极值。
已知直线
(I)若以点
为圆心的圆与直线
相切与点
,且点
在
轴上,求该圆的方程;
(II)若直线
关于x轴对称的直线为
,问直线
与抛物线
是否相切?说明理由.
已知函数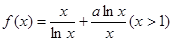 的图象经过
的图象经过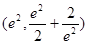
 其中
其中 为自然对数的底数,
为自然对数的底数,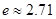
 .
.
(Ⅰ)求实数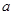 ;
;
(Ⅱ)求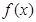 的单调区间;
的单调区间;
(Ⅲ)证明:对于任意的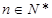 ,都有
,都有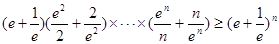 成立.
成立.
已知双曲线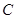 :
: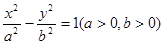 的右焦点为
的右焦点为 ,
, 在
在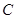 的两条渐近线上的射影分别为
的两条渐近线上的射影分别为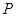 、
、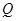 ,
, 是坐标原点,且四边形
是坐标原点,且四边形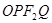 是边长为
是边长为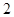 的正方形.
的正方形.
(Ⅰ)求双曲线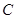 的方程;
的方程;
(Ⅱ)过 的直线
的直线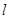 交
交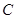 于
于 、
、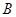 两点,线段
两点,线段 的中点为
的中点为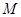 ,问
,问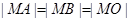 是否能成立?若成立,求直线
是否能成立?若成立,求直线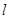 的方程;若不成立,请说明理由.
的方程;若不成立,请说明理由.
数列 中,
中, ,
, ,
, .
.
(Ⅰ)证明:数列 是等比数列,并求
是等比数列,并求 ;
;
(Ⅱ)求数列 的前
的前 项和
项和 .
.