定义:设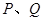 分别为曲线
分别为曲线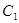 和
和 上的点,把
上的点,把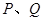 两点距离的最小值称为曲线
两点距离的最小值称为曲线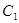 到
到 的距离.
的距离.
(1)求曲线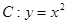 到直线
到直线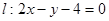 的距离;
的距离;
(2)已知曲线 到直线
到直线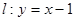 的距离为
的距离为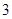 ,求实数
,求实数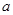 的值;
的值;
(3)求圆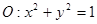 到曲线
到曲线 的距离.
的距离.
从某校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),……,第八组[190.195],下图是按上述分组方法得到的频率分布直方图.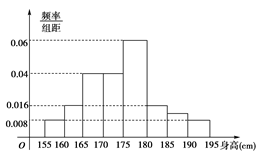
(1)求第七组的频数。
(2)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(本小题满分为12分)已知函数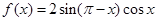 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
设函数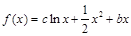
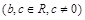 ,且
,且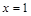 为
为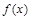 的极值点.
的极值点.
(Ⅰ) 若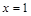 为
为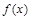 的极大值点,求
的极大值点,求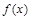 的单调区间(用
的单调区间(用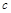 表示);
表示);
(Ⅱ) 若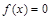 恰有两解,求实数
恰有两解,求实数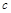 的取值范围.
的取值范围.
已知椭圆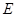 :
: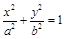 (
(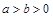 )过点
)过点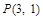 ,其左、右焦点分别为
,其左、右焦点分别为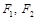 ,且
,且 .
.
(Ⅰ)求椭圆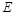 的方程;
的方程;
(Ⅱ)若 是直线
是直线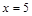 上的两个动点,且
上的两个动点,且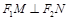 ,则以
,则以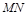 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.
已知数列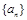 满足
满足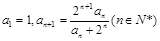 .
.
(Ⅰ)证明数列 是等差数列;
是等差数列;
(Ⅱ)求数列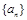 的通项公式;
的通项公式;
(Ⅲ)设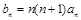 ,求数列
,求数列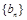 的前
的前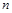 项和
项和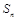 .
.