设函数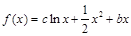
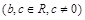 ,且
,且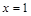 为
为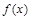 的极值点.
的极值点.
(Ⅰ) 若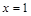 为
为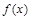 的极大值点,求
的极大值点,求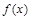 的单调区间(用
的单调区间(用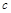 表示);
表示);
(Ⅱ) 若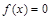 恰有两解,求实数
恰有两解,求实数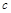 的取值范围.
的取值范围.
(本小题满分12分)如图,在四棱锥P –ABCD中,PA 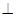 平面ABCD,
平面ABCD,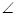 DAB为直角,AB//CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
DAB为直角,AB//CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
(Ⅰ)证明:AB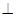 平面BEF:
平面BEF:
(Ⅱ)设PA =h,若二面角E-BD-C大于45  ,求h的取值范围.
,求h的取值范围.
(本小题满分12分)已知函数  在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增;如图,四边形OACB中,a,b,c为△ABC的内角以B, C的对边,且满足
上单调递增;如图,四边形OACB中,a,b,c为△ABC的内角以B, C的对边,且满足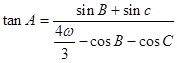 .
.
(Ⅰ)证明:b+c =2a:
(Ⅱ)若b=c,设 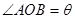 .
. ,求四边形OACB面积的最大值.
,求四边形OACB面积的最大值.
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|3x+2|
(Ⅰ)解不等式 ,
,
(Ⅱ)已知m+n=1(m,n>0),若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系 中,圆C的参数方程
中,圆C的参数方程 为参数).以
为参数).以 为极点,x轴的非负半轴为极轴建立极坐标系.
为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求曲线 的极坐标方程;
的极坐标方程;
(Ⅱ)设直线 极坐标方程是
极坐标方程是 射线
射线 与圆C的交点为
与圆C的交点为 、
、 ,与直线
,与直线 的交点为
的交点为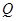 ,求线段
,求线段 的长.
的长.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,已知圆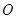 外有一点
外有一点 ,作圆
,作圆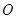 的切线
的切线 ,
,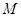 为切点,过
为切点,过 的中点
的中点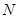 ,作割线
,作割线 ,交圆于
,交圆于 、
、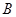 两点,连接
两点,连接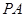 并延长,交圆
并延长,交圆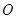 于点
于点 ,连接
,连接 交圆
交圆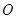 于点
于点 ,若
,若 .
.
(Ⅰ)求证:△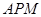 ∽△
∽△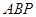 ;
;
(Ⅱ)求证:四边形 是平行四边形.
是平行四边形.