已知函数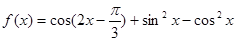 ,
,
(1)求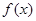 的对称轴方程;
的对称轴方程;
(2)用“五点法”画出函数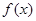 在一个周期内的简图;
在一个周期内的简图;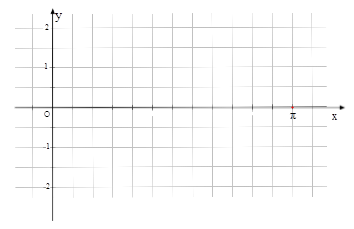
(3)若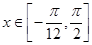 ,设函数
,设函数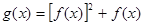 ,求
,求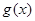 的值域。
的值域。
设函数 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若 的解集为
的解集为 ,
, ,求证:
,求证: .
.
在直角坐标系 中,已知圆
中,已知圆 的参数方程为
的参数方程为 为参数
为参数 ,以
,以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)已知直线 ,射线
,射线 .射线
.射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
如图, 为⊙
为⊙ 外一点,
外一点, 交⊙
交⊙ 于
于 ,
, ,
, 切⊙
切⊙ 于
于 为线段
为线段 的中点,
的中点, 交⊙
交⊙ 于
于 ,线段
,线段 的延长线与⊙
的延长线与⊙ 交于
交于 ,连接
,连接 .求证:
.求证:
(Ⅰ) ∽
∽ ;
;
(Ⅱ) .
.
已知函数 为常数,
为常数, 是自然对数的底数.
是自然对数的底数.
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)当 ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围.
的取值范围.
已知椭圆 的焦点在
的焦点在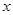 轴上,离心率等于
轴上,离心率等于 ,且过点
,且过点 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)过椭圆 的右焦点
的右焦点 作直线
作直线 交椭圆
交椭圆 于
于 两点,交
两点,交 轴于
轴于 点,若
点,若 ,求证:
,求证: 为定值.
为定值.