设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程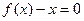 有实数
有实数
根;②函数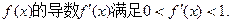 ”
”
(I)判断函数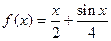 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中 的元素
的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意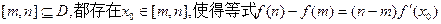 成立。试用这一性
成立。试用这一性
质证明:方程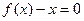 只有一个实数根;
只有一个实数根;
(III)对于M中的函数 的实数根,求证:对于
的实数根,求证:对于 定义
定义
域中任意的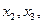 当
当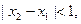 且
且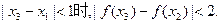
已知等差数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
(1)证明二维形式的柯西不等式:
(2)若实数 满足
满足 求
求 的取值范围.
的取值范围.
在极坐标系中,圆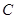 的圆心坐标为
的圆心坐标为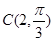 ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为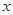 的正半轴,取相同的长度单位建立平面直角坐标系,
的正半轴,取相同的长度单位建立平面直角坐标系,
直线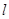 的参数方程为
的参数方程为 (
(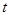 为参数)
为参数)
(1)求圆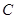 的极坐标方程
的极坐标方程
(2)设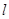 与圆
与圆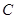 的交点为
的交点为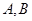 ,
,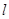 与
与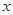 轴的交点为
轴的交点为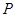 ,求
,求 .
.
如图,矩形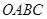 和平行四边形
和平行四边形 的部分顶点坐标为:
的部分顶点坐标为: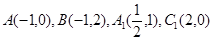 .
.
(1)求将矩形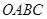 变为平行四边形
变为平行四边形 的线性变换对应的矩阵
的线性变换对应的矩阵 ;
;
(2)矩阵 是否存在特征值?若存在,求出矩阵
是否存在特征值?若存在,求出矩阵 的所有特征值及其对应的一个特征向量;若不存在,请说明理由.
的所有特征值及其对应的一个特征向量;若不存在,请说明理由.
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件:  .
.
(ⅰ)求 的值;
的值;
(ⅱ)若点 , 判断
, 判断 三点是否可以构成直角三角形?请说明理由.
三点是否可以构成直角三角形?请说明理由.