(1)已知函数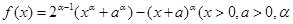 为有理数且
为有理数且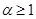 ),求函数
),求函数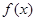 的最小值;
的最小值;
(2)①试用(1)的结果证明命题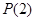 :设
:设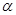 为有理数且
为有理数且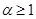 ,若
,若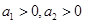 时,则
时,则 ;
;
②请将命题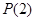 推广到一般形式
推广到一般形式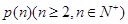 ,并证明你的结论;
,并证明你的结论;
注:当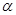 为正有理数时,有求导公式
为正有理数时,有求导公式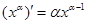
如图, 已知边长为2的的菱形 与菱形
与菱形 全等,且
全等,且 ,平面
,平面 平面
平面 ,点
,点 为
为 的中点.
的中点.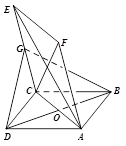
(Ⅰ)求证: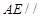 平面
平面 ;
;
(Ⅱ)求证: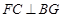 ;
;
(Ⅲ)求三棱锥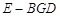 的体积.
的体积.
某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图。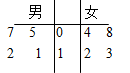
(Ⅰ)求样本的平均数;
(Ⅱ)设该题得分大于样本的平均数为合格,根据样本数据估计该校高三年级有多少名同学此题成绩合格;
(Ⅲ)在这4名男生和4名女生中,分别随机抽取一人,求该题女生得分不低于男生得分的概率.
已知数列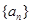 为等差数列,
为等差数列,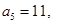 且
且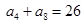 .
.
(Ⅰ)求数列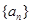 的通项;
的通项;
(Ⅱ)设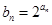
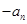 ,求数列
,求数列 的前
的前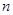 项和
项和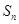 .
.
已知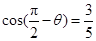 ,
,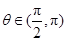 .
.
(Ⅰ)求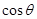 的值;
的值;
(Ⅱ)求函数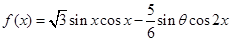 的增区间.
的增区间.
已知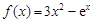 ,函数
,函数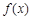 的零点从小到大依次为
的零点从小到大依次为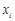 ,
,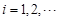 .
.
(Ⅰ)若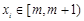 (
(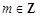 ),试写出所有的
),试写出所有的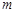 值;
值;
(Ⅱ)若 ,
,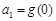 ,
,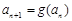 ,求证:
,求证:  ;
;
(Ⅲ)若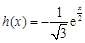 ,
, ,
,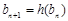 ,试把数列
,试把数列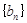 的前
的前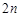 项及
项及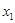 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).