如图， 为 直径，直线 与 相切于 . 垂直于 于 ， 垂直于 于 ， 垂直于 ，连接 .
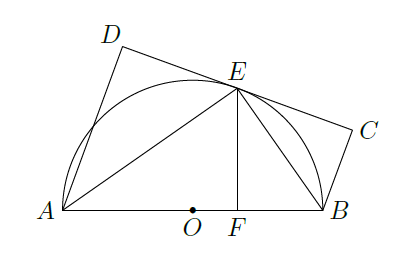
证明：
（I） ;
（II） .
函数
的图象记为E.过点
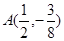作曲线E的切线，这样的切线有且仅有两条，求
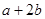的值.
为了降低能源损耗，某体育馆的外墙需要建造隔热层．体育馆要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度
（单位：cm）满足关系：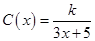
(
，
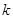为常数)，若不建隔热层，每年能源消耗费用为8万元．设
为隔热层建造费用与20年的能源消耗费用之和．
（1）求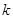的值及的表达式；
（2）隔热层修建多厚时，总费用达到最小？并求出最小值．
证明：
.
已知实数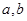
满足
，证明：
.
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组：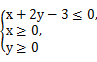
所表示的平面区域内的概率.