经销商经销某种农产品,在一个销售季度内,每售出
该产品获利润
元,未售出的产品,每
亏损
元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了
该农产品.以
(单位:
,
)表示下一个销售季度内经销该农产品的数量,
表示利润.

(Ⅰ)将
表示为
的函数
(Ⅱ)根据直方图估计利润
不少于
元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若
,则取
,且
的概率等于需求量落入
,求
的数学期望.
沪杭高速公路全长166千米,假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州。已知该汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 (千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(1)把全程运输成本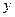 (元)表示为速度
(元)表示为速度 (千
(千 米/时)的函数,并指出这个函数的定义域;
米/时)的函数,并指出这个函数的定义域;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?
已知函数
(1)求曲线 在点
在点 处的切线的方程;
处的切线的方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标。
的方程及切点坐标。
命题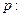 实数
实数 满足
满足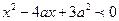 ,其中
,其中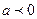 ;命题
;命题 实数
实数 满足
满足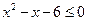 或
或 ,且
,且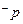 是
是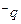 的必要不充分条件,求
的必要不充分条件,求 的取值范围
的取值范围
设 ,
, ,
,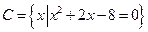 ,
, ,且
,且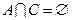 ,求
,求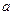 的值;
的值;
(本小题共12分)设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式,(用a表示b),并求f(x)的单调区间。
⑵设a>0, 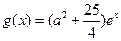 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。