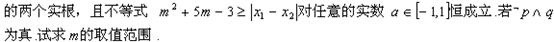平面直角坐标系
中,过椭圆
右焦点的直线
交
于
两点,
为
的中点,且
的斜率为 .
.
(Ι)求
的方程;
(Ⅱ)
为
上的两点,若四边形
的对角线
,求四边形面积的最大值
(本小题满分10分)选修4-1:几何证明选讲
如图15-58,已知PA是⊙O的切线,A为切点,PBC是过O的割线,PA=10,PB=5,∠BAC的平分线BC和⊙O分别交于点D、E.
求(1)⊙O的半径;(2)sin∠BAP的值;(3)AD·AE的值
(本小题满分12分)
已知函数
(1)如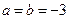 ,求
,求 的单调区间;
的单调区间;
(2)若 在
在 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
(本小题满分12分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动.若厂家投放A、B型号电视机的价值分别为p、q万元,农民购买电视机获得相应的补贴分别为 已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据:
已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据: ).
).
(1) 请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况.
(本小题满分12分) 已知函数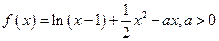 .
.
(I)若f(x)存在单调递减区间,求a的取值范围;
(Ⅱ)记f(x)在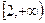 的最小值为f(t),求t的值。
的最小值为f(t),求t的值。