设
均为正数,且
,证明:
(Ⅰ)
;
(Ⅱ)
(本小题满分12分)
如图,四棱椎P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是300,点F是PB的中点,点E在边BC上移动 。
。
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有AF⊥PE;
(3)求当BE的长为多少时,二面角P-DE-A的大小为450。
(本小题满分12分)
在数列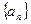 中,已知
中,已知 且
且 。
。
(1)记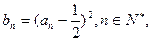 证明:数列
证明:数列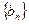 是等差数列,并求数列
是等差数列,并求数列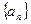 的通项公式;
的通项公式;
(2)设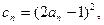 求
求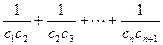 的值。
的值。
(本小题满分12分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,先从这个盒子中有放回地先后抽取两张卡片,设这两张卡片的号码分别为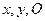 为坐标原点,
为坐标原点,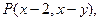 记
记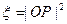
(1)求随机变量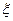 的最大值,并求事件“
的最大值,并求事件“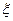 取最大值”的概率;
取最大值”的概率;
(2)求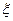 的分布
的分布 列及数学期望。
列及数学期望。
(本小题满分10分)
已 知函数
知函数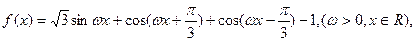 且函数
且函数
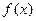 的最小正周期为
的最小正周期为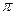 ;
;
(1)求函数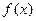 的解析式;
的解析式;
(2)在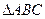 中,角
中,角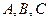 所对的边分别为
所对的边分别为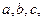 若
若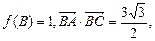 且
且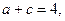 求
求 的值。
的值。
已知圆C1的方程为 ,椭圆C2的方程为
,椭圆C2的方程为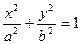
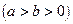 ,C2的离心率为
,C2的离心率为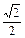 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线A
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线A B的
B的 方程和椭圆C2的方程.
方程和椭圆C2的方程.