甲
乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是
外,其余每局比赛甲队获胜的概率都是
.假设各局比赛结果相互独立.
(Ⅰ)分别求甲队以
胜利的概率;
(Ⅱ)若比赛结果为求
或
,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分
对方得1分.求乙队得分
的分布列及数学期望.
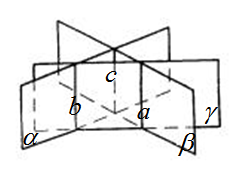
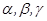 是空间不重合的平面,且
是空间不重合的平面,且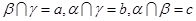 ,且
,且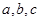 是不重合的直线,求证:
是不重合的直线,求证: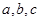 交于一点或
交于一点或 ∥
∥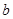 ∥
∥ .
.
在△ABC中,A,B,C所对的边分别是
(1)用余弦定理证明:当C为钝角时, ;
;
(2)当钝角△ABC的三边 是三个连续整数时,求△ABC外接圆的半径.
是三个连续整数时,求△ABC外接圆的半径.
如图,已知 与圆
与圆 相切于点
相切于点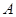 ,经过点
,经过点 的割线
的割线 交圆
交圆 于点
于点 、
、 ,∠APC的平分线分别交
,∠APC的平分线分别交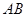 、
、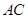 于点
于点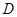 、
、 .
.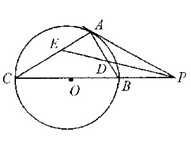
(1)证明:∠ADE=∠AED;
(2)若AC=AP,求 的值.
的值.
正方体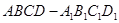 中,连接
中,连接 .
.
(1)求证: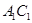 ∥平面
∥平面 ;
;
(2)求证:平面 ∥平面
∥平面 ;
;
(3)设正方体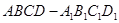 的棱长为
的棱长为 ,求四面体
,求四面体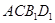 的体积.
的体积.
如图,四棱锥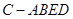 中,四边形
中,四边形 是正方形,若
是正方形,若 分别是线段
分别是线段 的中点.
的中点.
(1)求证: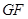 ||底面
||底面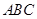 ;
;
(2)若点 为线段
为线段 的中点,平面
的中点,平面 与平面
与平面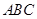 有怎样的位置关系?并证明。
有怎样的位置关系?并证明。