椭圆
:
的左
右焦点分别是
,离心率为
,过
且垂直于
轴的直线被椭圆
截得的线段长为1.
(Ⅰ)求椭圆
的方程;
(Ⅱ)点
是椭圆
上除长轴端点外的任一点,连接
,设
的角平分线
交
的长轴于点
,求
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点 作斜率为 的直线 ,使 与椭圆 有且只有一个公共点,设直线的 斜率分别为 .若 ,试证明 为定值,并求出这个定值.
(12′)已知集合A ,B
,B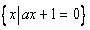 ,且
,且 ,求实数
,求实数 的值组成的集合
的值组成的集合
(选修4—5:不等式选讲)设函数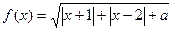 。
。
(1)当a=-5时,求函数 的定义域。
的定义域。
(2)若函数 的定义域为R,求实数a的取值范围。
的定义域为R,求实数a的取值范围。
(选修4—4:坐标系与参数方程)设直角坐标系的原点与极坐标系的极点重合,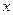 轴正半轴与极轴重合。已知圆C的极坐标方程:
轴正半轴与极轴重合。已知圆C的极坐标方程: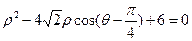
(I)将极坐标方程化为普通方程。
(II)若点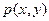 在圆C上,求
在圆C上,求 的取值范围。
的取值范围。
如图,BA是⊙O的直径,AD是⊙O切线,C、E分别
为半圆上不同的两点,BC交AD于D,BE交AD于F。
(I) 求证:BE·BF=BC·BD。
(II) 若⊙O的半径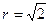 ,BC=1,求AD。
,BC=1,求AD。
设函数 ,
,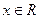 。
。
(1)求函数 的单调区间和极值。
的单调区间和极值。
(2)若关于 的方程
的方程 ="a" 有三个不同实根,求实数a的取值范围。
="a" 有三个不同实根,求实数a的取值范围。
(3)已知当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。