已知数列 满足
满足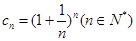 ,试证明:
,试证明:
(1)当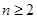 时,有
时,有 ;
;
(2) .
.
(本小题满分12分)
已知函数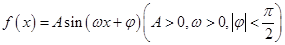 的图象与
的图象与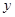 轴交点的纵坐标为1,在相邻的两点
轴交点的纵坐标为1,在相邻的两点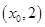 ,
,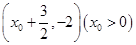 上
上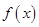 分别取得最大值和最小值.
分别取得最大值和最小值.
(1)求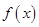 的解析式;
的解析式;
(2)若函数 的最大和最小值分别为6和2,求
的最大和最小值分别为6和2,求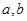 的值.
的值.
(本小题满分12分)
已知
(1)化简 ;
;
(2)若 是第三象限角,且
是第三象限角,且 ,求
,求 的值;
的值;
(3)若 ,求
,求 的值.
的值.
(本小题满分12分)
已知 是方程
是方程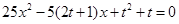 的两根且
的两根且 为锐角,求t的值.
为锐角,求t的值.
(本小题满分12分)
若 是偶函数,
是偶函数, 为常数,且
为常数,且 的最小值是0.
的最小值是0.
(1)求 的值;
的值;
(2)求 的最大值及此时
的最大值及此时 的集合.
的集合.
(本小题满分12分)
有两枚大小相同质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5。同时投掷这两枚玩具一次,记m为两个朝下的面上的数字之和.
(1)求事件“m不小于6”的概率 ;
(2) “m为奇数”的概率和“m为偶数”的概率是否相等?证明你做出的结论.