如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角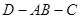 ,如图二,在二面角
,如图二,在二面角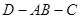 中.
中.
(1) 求CD与面ABC所成的角正弦值的大小;
(2) 对于AD上任意点H,CH是否与面ABD垂直。
已知等差数列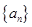 满足:
满足: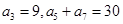 ,
,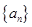 的前n项和为
的前n项和为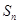 .
.
(1)求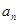 及
及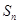 ;
;
(2)已知数列 的第n项为
的第n项为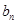 ,若
,若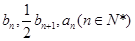 成等差数列,且
成等差数列,且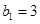 ,设数列
,设数列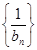 的前
的前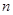 项和
项和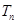 .求数列
.求数列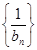 的前
的前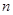 项和
项和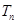 .
.
设有关于x的一元二次方程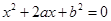 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
设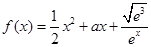 .
.
(1)若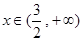 时,
时,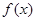 单调递增,求
单调递增,求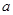 的取值范围;
的取值范围;
(2)讨论方程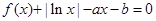 的实数根的个数.
的实数根的个数.
已知椭圆C的中心在原点,焦点F在 轴上,离心率
轴上,离心率 ,点
,点 在椭圆C上.
在椭圆C上.
(1)求椭圆 的标准方程;
的标准方程;
(2)若斜率为
 的直线
的直线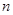 交椭圆
交椭圆 与
与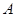 、
、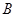 两点,且
两点,且 、
、 、
、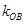 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求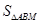 的最大值.
的最大值.
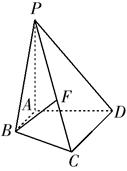
如图,已知四棱锥 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形, ,且
,且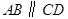 ,
,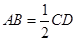 .
.
(1)点 在线段
在线段 上运动,且设
上运动,且设 ,问当
,问当 为何值时,
为何值时, 平面
平面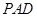 ,并证明你的结论;
,并证明你的结论;
(2)当 面
面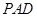 ,且
,且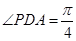 ,
,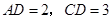 求四棱锥
求四棱锥 的体积.
的体积.