如图, 四棱柱
的底面
是正方形,
为底面中心,
平面
,
.

(Ⅰ) 证明:
平面
;
(Ⅱ) 求平面
与平面
的夹角
的大小.
(本小题满分14分)
已知定义域为 的函数
的函数 是偶函数,当
是偶函数,当 时,
时, .
.
(1)求 的解析式;
的解析式;
(2)证明方程 在区间
在区间 上有解
上有解
(本小题满分14分)
某地区在高一年级学完《数学必修1》后进行评估测试.现从所有参加测试的全体学生中随机抽取500名学生的试卷进行统计分析,就学生的成绩制成频率分布直方图(如图).
(1)在这500名学生中,成绩不低于80分的有多少人?
(2)设成绩不低于60分为合格,求这次评估测试的合格率;
(3)估计这次评估测试的平均分.
(本小题满分12分)
已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹
的轨迹 为
为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)过点F2(1 ,0)作直线l与轨迹
,0)作直线l与轨迹 交于不同的两点A、B,设
交于不同的两点A、B,设
 ,若
,若 的取值范围
的取值范围
(本小题满分12分)
设数列 的前
的前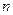 项和为
项和为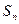 ,且
,且 数列
数列 满足
满足 ,点
,点 在直线
在直线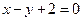 上,
上,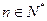 .
.
(Ⅰ)求数列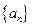 ,
, 的通项公式;
的通项公式;
(Ⅱ)设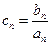 ,求数列
,求数列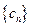 的前
的前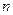 项和
项和 .
.
如图所示,某公园预计在一块绿地的中央修建两个相同的矩形的池塘,每个面积为10000米2,池塘前方要 留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?
留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?