给定常数
,定义函数
,数列
满足
.
(1)若
,求
及
;
(2)求证:对任意
;
(3)是否存在
,使得
成等差数列?若存在,求出所有这样的
,若不存在,说明理由.
(本小题满分12分)已知函数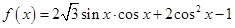 .
.
(Ⅰ)求函数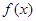 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.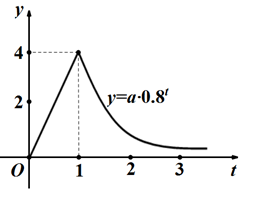
(Ⅰ)写出第一次服药后 与
与 之间的函数关系式
之间的函数关系式 ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: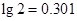 ).
).
(本小题满分12分)已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
(本小题满分12分)已知向量 ,
, ,设
,设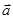 与
与 的夹角为
的夹角为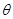 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求 的值.
的值.
(本小题满分12分)已知幂函数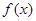 的图象经过点
的图象经过点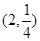 .
.
(Ⅰ)求函数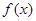 的解析式;
的解析式;
(Ⅱ)判断函数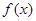 在区间
在区间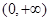 上的单调性,并用单调性的定义证明.
上的单调性,并用单调性的定义证明.